Battleships, Beatles and Body parts

Have you ever wondered how doctors can take pictures in slices through the body? Being able to see how the various parts in your body look in cross section is a useful aid to diagnosis, but you can't slice someone open just to have a peak, you need to use technology to let you see inside. The story of how this important Nobel Prize winning medical breakthrough became a medical reality involves some clever rediscovered maths, computers and a 60's boy band!

Me and my X-ray shadow

In a normal X ray you stand in front of a photographic plate, and then X-rays shine through you onto the plate behind. Your bones, containing lots of calcium, have a higher density than the flesh and muscle surrounding it, so in effect you get a bone shadow being cast on the photographic plate; the bones have absorbed the X-rays. Useful as X-rays are, the problem is that you only get to know how much bone an X-ray has gone through and nothing about where that bone was along the X-ray's journey. The shadow is flat, but your body is 3D.

Let's play battleships

While you are wondering how we can do 3D scans of the body, let's take a break and play a game of Battleships. Battleships is a pencil and paper game that's been around for ages. Using a square grid of paper, with the rows and columns labelled, you and a mate decide where on your grids you are going to position your 'fleet'. A fleet consists of a number of different types of ships: a battleship normally takes up 4 squares, either horizontally or vertically, a cruiser (a smaller type of ship), takes up say only 2 squares and a destroyers normally 1 square. At the start you decide how many of each type of ship you will both have in a fleet, and secretly position them on your grid. The rules are you take it in turns to 'fire' at your opponent's grid. For example you might fire on position B9. That's the square in row B and column 9. If that grid location is a part of one of your ships, it's a hit. You have to admit it and say what type of ship it is, and then give your opponent another go. This way players can try and discover for example whether the 4 grid battleship is positioned horizontally or vertically. The first player to sink all of the other person's fleet wins. Those 1 square destroyers are the hardest to get of course, as you need to fire right on top of them to sink them.

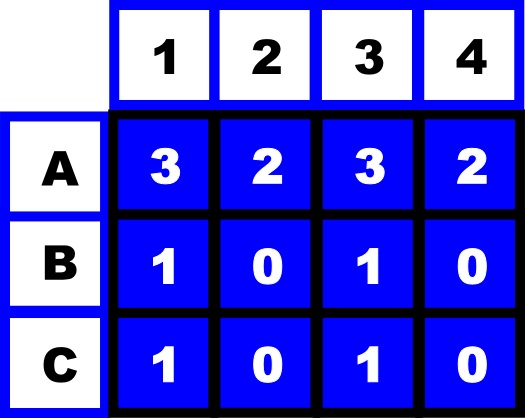
Pond life

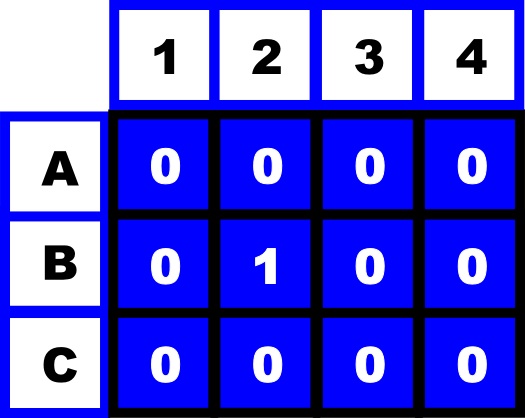
Imagine a much smaller game of battleships as shown here. Rather than an ocean it's a pond. There is one destroyer (indicated by the number 1 in a sea of zeros) at grid location B2.

You might be lucky and hit B2 on your first shot, or it may take a long process of elimination to find it. Is there another way you could find where the 1 is?

I see no ships, so give us a clue

The answer is yes, but only if you could get your opponent to give you some simple clues. Then you could work it out. First you get them to add up all the values along the rows. You would get the information: Row A=0, Row B=1 (as it's 0+1+0+0) and Row C=0 . That is a start. You now know the ship is on row B but you don't know where on row B it is. So you now ask for the sum down the columns Column 1 = 0, Column 2=1, Column 3=0 and Column 4=0. You now know its in column number 2. Combining this information, gives you the location as being grid position B2, and BANG, its sunk!

A guide to automatic ship finding

Now suppose there are 2 destroyers somewhere in the grid (to cheat and see what this grid actually is follow this link). Your friend gives you the sums along the rows and down the columns again. This time it's Row A=2, Row B=0 and Row C=0 ; Column 1=1, Column 2=0, Column 3=1 and Column 4=0. Where are the ships?

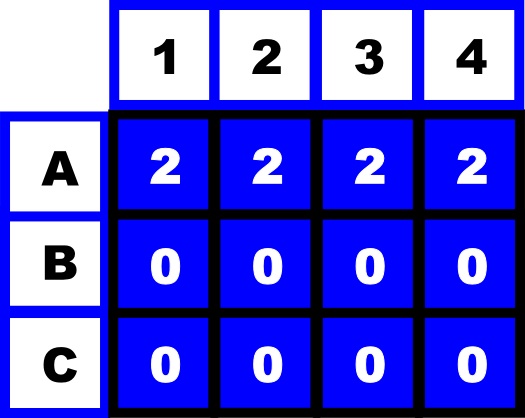
I know that in row A the total is 2. There is something in there! If we start with a grid of zeros we can spread the information that there is something in Row A all the way along row A so we have:

Though we have smeared the data along the row we still don't know where the 'something' in Row A is yet, just that it's in there somewhere. We can do this smearing for Row B and Row C, not much extra information here as they both had totals of zero.

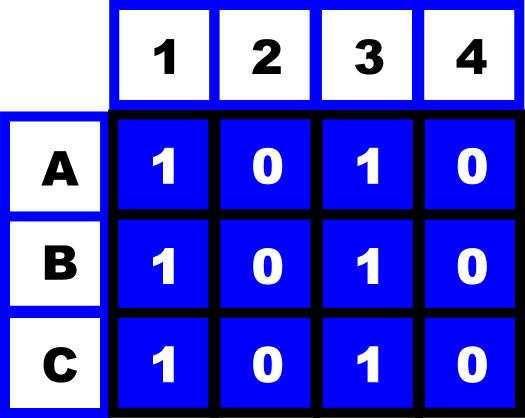
We know there was something in Row A and that's what this shows, but we still don't know where those somethings are. Now we look at the columns and create a new grid. If we do the same smearing of the information down the columns: remember Column 1=1, Column 2=0 Column 3=1 and Column 4=0, we get:

We know there is something in columns 1 and 3, but not where in that column they are. To finally solve the problem and recover the location of the ships we just add these two grids with the smeared information together to get.

Where for example A2 = 2+0. If we now look at this added together grid with the two sets of smeared data there are two peaks, of value 3, in positions A1 and A3. The peaks give the locations of the ships. We have an automatic ship finder but more importantly we have a way of recovering the actual position of the ships in the grid, reconstructing the game board in effect. We get it by using a set of results produced by adding together all the information along a row or a column. Now its time to weigh anchor and get back to the X-rays. As you probably guessed that is what we were really working on all along.

An X-ray marks the spot

As an X-ray passes straight through your body it is absorbed by all the bits of bone in the way, so in effect at a particular point on the X-ray plate you have something similar to adding together all the 'ships' (bits of bone) along its journey (say a row of the game board). So our X-ray is in fact like the set of numbers Row A=2, Row B=0 and Row C=0, we know that the ray arriving at position A has gone through more bone (ships) than the rays going along Row B or C. But we want to know how these bits of bones are related to one another. Are they close together or far apart. Both would give the same amount of absorption. So like our ship finder above we can rotate the X-ray source around the patient, so that it's coming in from the top rather than the side, and take another X-ray. This time our X-ray plate will show information of the form Column 1=1, Column 2=0 Column 3=1 and Column 4=0. We can then take these two X-rays, do the smearing process (which is called 'back projection' as you are smearing the data back to where it came from), and add the two back projected images together. In the same way as the ship detector was able to find where the ships were in the grid this mathematics tells you where the bits of bone were located in the body. And you don't need to just do 2 scans, you can rotate the X-ray source around the body taking thin scans at lots of different angles, then back project and add, so building a high quality image of a thin slice through the body.

The Beatles CAT

This method is called CAT: Computer Assisted Tomography (tomos is Greek for a slice). The EMI Scanner was the first commercially viable CAT technology, and was developed by the record company Thorn EMI back in the 1960s. The story goes that they were able to fund this expensive medical research because of the money they made from the pop group The Beatles: the Take That of their day. They needed to find some way to spend the enormous amount of money they were making! The mathematics for back projection had been around for a long time, it was called the 'Radon transform', but until the medical applications and more importantly the computers came along that could calculate this maths in a reasonable time it had lain undiscovered.

The inventor of the EMI Scanner was jointly awarded the Noble Prize for Medicine for his efforts. Tomography is now used routinely in medicine, but is also used in archaeology to see inside Egyptian mummies, for example, and in geophysics where you want to take slices through the earth. It's another example of how mathematics, computer science and engineering can all come together at the right time to change the way the medical world works.

Anyone for a game of tomographic battleships?