Marks for the da Vinci Code: B-

Dan Brown's book "The da Vinci Code" has become one of the best selling books of all time. It's a thriller but controversially includes a claim that it is largely based on fact. Professor Harold Thimbleby of the Department of Computer Science at Swansea University, tells us why he grades it down for science and how Dan Brown missed some interesting true science.

The da Vinci Code became a publishing phenomenon, not least because of its innacurate and controversial version of early Christian history. We can allow fiction authors creative freedom to change history to get a good story, but why do they mangle the science? Especially when getting it right would have been even more interesting! Dan Brown puts silly words into the mouths of his "expert" characters: a Harvard professor, a graduate of the Royal Holloway College's leading security course, and a top historian.

Even Dan Brown's "facts" about bee keeping are wrong. This may be quibbling, but the moral is that readers of novels should be cynical or risk believing complete fabrications - hard to do when the story is so exciting, and the overwhelming desire is to turn the page. Even when under pressure though, a scientist should check their facts - or they risk getting stung.

The book is very exciting with police chases, murderers, mysterious clues ... It starts off with a particularly nasty murder in the Paris Louvre. A Harvard professor, Robert Langdon, is a key suspect. The victim managed to scrawl some numbers on the floor next to his naked body. Perhaps he has written a clue to who the murderer was? Sophie Neveu, a cryptographer, recognises the numbers for what they are. They are a special sequence called "The Fibonacci numbers", 1 1 2 3 5 8 13 21 ..., but they'd been written down in a mysterious order as 13-3-2-21-1-1-8-5.

Soon the Harvard professor is daydreaming about a lecture he gave to his students on the divine proportion, which he calls "PHI" though it's usually known as the Golden Ratio. There's nothing especially divine about it, unless you are writing a theological consipracy thriller! Its value is approximately 1.618. It is what a mathematician would call an "irrational" number: the digits go on for ever after the decimal point, and writing its numerical value down exactly is impossible. So despite the da Vinci Code's excitement about many amazing things being exactly equal to PHI that is simply not possible!

The Golden Ratio turns up for good reasons in many surprising places because it is the solution of a simple and common equation. It even turns up in bee hives, which is a point Dan Brown tries to make. Unfortunately he gets it quite wrong and misses a much more interesting (and true) story.

Bees?

Let's pick up the story directly from the book:

"Plants, animals and even human beings all possessed dimensional properties that adhered with eerie exactitude to the ratio of PHI to 1 ... So the ancients assumed PHI must have been preordained by the Creator ..."

Langdon grinned. "Ever study the relationship between female and males in a honeybee community?"

"Sure. The female bees always outnumber the male bees."

"And did you know that if you divide the number of female bees by the number of male bees in any beehive in the world, you always get the same number?"

"You do?"

"Yup. PHI."

The girl gaped. "No way!"

This couldn't be more wrong, especially the so-called eerie exactitude! Approximately 95% of a bee hive are workers, and the workers are female, so that leaves 5% males. If you divide 95 by 5 you get 19, which is nothing like "the ratio of PHI to 1", 1.618. Hardly an eerie exactitude! And in a severe winter, all the male bees die off, so then the ratio is infinite! So the facts seem to make Dan Brown completely wrong. But did he somehow hear something interesting about bees and the Golden Ratio but lost it in the retelling?

Langdon goes on to claim that the human body is made of building blocks whose proportion is always equal to PHI. He tells his students to take a tape measure into the shower to check his claims. Like any good scientist, I did. And, again, he's wrong. I did come up with some other interesting numbers, though!

Two Bees or Not Two Bees?

Bees are very intriguing. A male bee, a drone, hatches from an unfertilised egg, whereas all females hatch from fertilised eggs. That means males have just one parent, who produced the egg. Females have two parents, the mother that produced the egg and the father that fertilized it.

(There are further complications in that some females are queens and some workers. Workers are sterile females, and usually have no offspring. In a hive there is normally one queen, busy laying maybe 2000 eggs a day. From time to time, there are females who are fed royal jelly and they grow into new queens. In a typical honey bee hive there will be tens of thousands of workers. When a successful hive gets too big, one or more queens will buzz off with a swarm of bees to start new hives somewhere else. This behaviour would be disastrous for a beekeeper, as they'd loose most of their bees, so well-managed bees are usually fooled into not swarming.)

Parents...

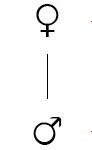
Let's try and work out what the facts about the female to male ratio are, and where Dan Brown might have got his ideas from. It's convenient to represent males and females by their usual signs, ♂ for males and ♀ for females. Now imagine a single male, who we'll call Rob. Now Rob, being a male, has one parent, the queen (a female). We can draw a family tree for this simple single parent family.

Grandparents...

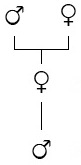
In turn, the queen, Rob's mother, being a female bee, had two parents. Now, let's expand the family tree further back to include Rob's grandparents.

Great-grandparents...

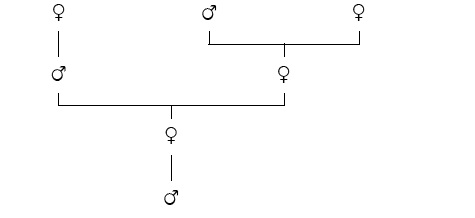
In the diagram, you can see that Rob has one parent (the queen), two grandparents (a drone and another queen, probably a queen from a hive far, far away). In turn these two grandparents have their own parents, who are Rob's great grand parents.

You may like to carry on drawing a few more generations back. Looking at Rob's family tree, count the number of bees in each generation. Start with the original bee, Rob. He has 1 parent. He has 2 grandparents, then 3 great grandparents, and, going beyond our drawing, then there will be 5 great great grandparents, 8 great great grandparents, 13 great great great grandparents, 21 great great great great grandparents. You can should draw the family trees to check. The murder victim's Fibonacci numbers have reappeared! 1 1 2 3 5 8 13 21...

Fibonacci numbers are easier to work out than counting Rob's ancestors. Each number in a Fibonacci sequence is the sum of the previous two. After two ones at the beginning, the next is 2, which is 1+1. After 2 comes 3, which is 1+2, adding the two numbers preceding it. After 3 comes 5, which is 2+3. Then 8, which is 3+5. In general, if two consecutive Fibonacci numbers are x and y, the next one is x+y.

Rabbits?

Curiously Fibonacci, the twelth century mathematician who invented Fibonacci numbers, originally got them through thinking about breeding rabbits, not bees! In fact, Fibonacci's rabbits were rather contrived to get the numbers to come out right, whereas our bees do what real bees do and the numbers work out just right. Perhaps Fibonacci did not know about bees? Although we now remember Fibonacci because of his numbers, he should also be remembered as the person who brought Arabic numbers to Europe. They replaced the ungainly Roman numerals that were used everywhere in those days. He made maths easier at a stroke.

So we've found a mathematical connection between bees and the mysterious Fibonnaci numbers. What about the Golden Ratio? Where is the connection Langdon was trying to make? What have Fibonnaci numbers got to do with Langdon's PHI, the Golden Ratio?

The Golden Ratio comes back in because the ratio of consecutive Fibonacci numbers get closer and closer to it. Try it: 1/1=1, 2/1=2, 3/2=1.5, 5/3=1.67, 8/5=1.6 ... Not enough evidence there to convince your? Write a computer program (or use a calculator) to work out the ratios a bit further to see them get closer.

So, the ratios certainly look like they get closer and closer to a number near 1.6180... Can we really be sure this eventually ends up at the Golden Ratio if we've only checked a few cases?

With a bit of more advanced maths you can actually work out that it is eventually exactly the Golden Ratio - that is the beauty of maths, you can prove things that are true about numbers, not just rely on testing it for a few of them and hoping it works for the rest.

So we have found an interesting fact linking Bees, Fibonnaci numbers and the Golden Ratio. It is just not the "fact" given in the story: it's nothing to do with male-female ratios in hives as the expert "Havard Professor" thought, it's to do with ratios in a bee's ancestors. There's another interesting problem we'll let you think about: as Fibonacci numbers get bigger and bigger, the number of Rob's ancestors far enough back in time must have been huge. Where did they all come from? Or have we overlooked something?

So, there you are, it's not "to be or not to be," so much as "two bee or 1.618 bee."

Brown's book starts with a big banner saying "Fact: ... all the descriptions of artwork, architecture, documents and secret rituals in this novel are accurate." No way. Perhaps we can look forward to a blockbuster of a book that starts off by saying "Fact: all the descriptions of artwork, architecture, science and maths, computers, documents and secret rituals in this novel are accurate." Ahh, that'd be nice!

The "secret ritual" of a scientist is to check facts, and, as we saw, in turn to check the implications of the facts we check. We learn a lot about bees if we do, and we realise there's still a lot more to discover and check ... which is how science weaves its story.