The remote control brain experiment: what's going on?

So you have done our remote control brain experiment. Is mind control a reality? Do you now believe in hocus pocus? Or are you instead looking for an explanation of why it always works?

Of course it's not mind control. It's mathematics, but you knew that didn't you? I thought you would. But how does this mind reading miracle work. Well its all down to Abracadabra algebra!

The set up - lets get abstract!

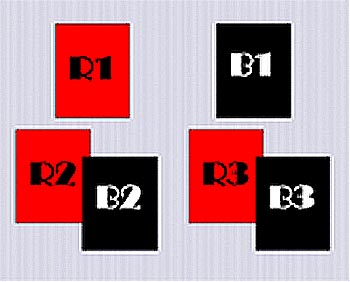
Let's call the number of cards in the two piles you dealt R1 for the red pile and B1 for the black pile. The two other piles in front of these contain a random mixture of red and black, so lets say that the pile in front of R1 contains R2 reds and B2 blacks, and the pile in front of B1 contains R3 reds and B3 blacks. See the picture.

So what do we know?

We actually ask in the first part of the experiment for you to divide the pack in half. You may have missed that but 8+7+6+5=26.

Now we also know that, for a full pack of 52 cards half (26) are red, and the other half are black so all the red counts add up to 26 and similarly the blacks:
R1 + R2 + R3 = 26 Call this equation (1)
B1 + B2 + B3 = 26 Call this equation (2)

We also know the number of cards in the RED pile (R1) is the same as the number of face down cards placed in front of it (made up of R2 red cards and B2 black cards) so together R2+B2 must add up to R1. Similar reasoning holds for the cards in front of the BLACK pile. So:
R1 = R2 + B2 Call this equation (3)
B1 = R3 + B3 Call this equation (4)

So if we substitute equation (3) in equation (1) eliminating R1 we get
(R2 + B2) + R2 + R3 = 26 Call this equation (5)

Similarly if we substitute equation (4) in equation (2) eliminating B1 we get
(R3 + B3) + B2 + B3 = 26 Call this equation (6)

Combining equations (5) and (6) as both add up to 26, we get
2xR2 + B2 + R3 = 26 = R3 + 2xB3 + B2

We can subtract R3 and B2 from each side. That leaves
2xR2 = 2xB3

We can divide both sides by 2 giving
R2 = B3

Now what did we say R2 and B3 stood for? The maths shows that the number of RED cards (R2) in front of the RED pile MUST ALWAYS be equal to the number of BLACK cards (B3) in front of the BLACK (B1) pile. That is how the magic works. Maths.

Testing times for self-working magic

The algebra proves the numbers will always be the same: so long as you follow the instructions for the trick (the algorithm) it will always work. The rest of the trick is just presentational flim-flam ... but don't tell anyone how it works!

Algebra is another way that we can test to see if computer programs will always do what we want them to, by taking the problem and turning it into an "abstraction". As we have done here abstraction uses general quantities such as R1 rather than say the actual number of cards, say 12. Using proof we can be sure that the trick will be self-working without having to try every single set of possible cards. After all, it may work 99% of the time but could you be sure that the one time you're trying to impress a friend it would not be the 1% it didn't work? I know what my luck is like! What if you were talking about, instead of a magic trick, a computer program that was controlling the landing gear on your plane. You would want to be sure that worked 100% of the time: that every time the program followed the instructions the right thing happened. Mathematical proof is at the core of computer science, helping create safer systems.