Magic Squares: Just run the numbers

by Peter McOwan, Queen Mary University of London

A magic square is a grid of numbers where each row, column and diagonal add up to the same number. To create them you need both patience and cunning... or maybe just an algorithm. In fact, there are lots of algorithms for building magic squares. Here is one for building lots of different 3x3 squares: giving you a way to display your skill in the magic square architecture field!

To build this type of magic square, follow the algorithm below:

1. First chose 9 consecutive numbers. If you chose numbers starting from 1, for example, that would mean, 1 to 9. These are the numbers that will go in your magic square. But where?
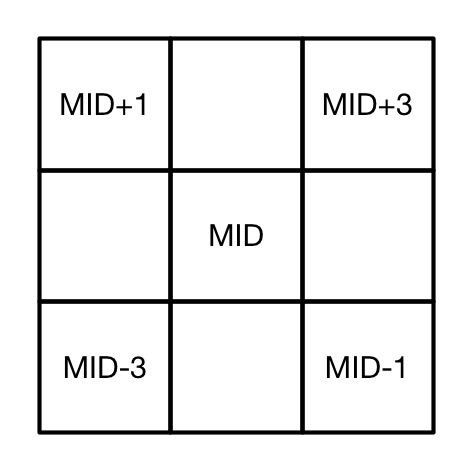
2. Next find the number in the middle of the 9 numbers you have chosen. We chose 1 to 9, so 5 is the number in the middle of this sequence. (It will always be 4 more than the starting number). Let's call this mid-sequence value MID, to allow us to be general when we follow the rest of the instructions.
3. Multiple the middle number, MID by 3, (so 5*3 = 15). That number, (15 for our example) will be the TARGET number that the square rows and so on will add to.
4. On a 3 by 3 grid, put MID in the centre square.
5. Place the number (MID + 3) in the upper right-hand square.
6. Place the number (MID - 3) in the lower left-hand square.
7. Place the number (MID + 1) in the upper left-hand square.
8. Place the number (MID - 1) in the lower right-hand square.
9. Fill in the remaining squares to make the magic square work.

For the last step, you just need to fill in the empty squares, to make sure the rows and columns add to the right number. To do this you just need to keep in mind the target magic number you calculated, TARGET (For our example, remember it was 15). It's a bit of simple arithmetic to find these final numbers and voila, you have built a magic square from the 9 numbers.

If you can practice doing the maths in your head you could turn this in to a magic trick, by getting a member of the audience to write down the intial sequence of numbers. You then turn them in to the magic square.

An alternative way to do the trick based on the same underlying pattern, is to get the audience member to pick a target number out of a hat. You then write out a magic square that adds to that number. The secret is to make sure all the numbers you put in the hat are mulitples of 3 (i.e. are in the 3 times table). You get MID just by dividing the number chosen by 3, and then following the last part of the above algorithm that tells you what numbers to put where in the grid.

To be an algorithm (and for you to always impress with your magic) it must ALWAYS work. How can we be sure it does. Can you prove it always does? Watch this space.