The Binary Secret of Nim

The secret of Nimrod, that astounded everyone at the Berlin Trade Fair is actually an algorithm that uses some cunning binary maths. You can see it in action by clicking on "Show Computer Thinking" in our Hamster Nim.

Count the hamsters and convert to binary

How does it work? Well first you count the hamsters in each pile. You then convert this number to binary - writing it out in base 2 instead of the normal base 10.

Add, then odd or even?

Next you add up the ones in each column (don't worry about carry's), and note whether the total for each is odd or even. Write down 0 under that column if it is even and write down a 1 if the total is odd. In computer science terms you have just done a binary operation called XOR (short for exclusive OR).

Winning or Losing Position?

It turns out that any state of play in a game of Nim can be thought of as a winning position or as a losing position. What that means is that there are some positions that the person to play can guarantee to win from if they make no mistakes (whatever the other player does). They can force a win. On the other hand, there are some positions that are guaranteed losing positions (unless the other player gets it wrong). Every move you can possibly make takes the game to a position where your opponent can force a win.

For example, if a game has got to to a state where there are only two piles and both have the same number of hamsters, then if its your turn you are in a losing position. Whatever number of hamsters you remove, your opponent can match them in the other pile. Eventually you end up taking the last hamster of your pile and your opponent takes the last one of all from the other pile and wins. So an identical number of hamsters in two piles is a losing position, but two piles with different numbers of pieces is a winning position.

Flip bits to win

With that sorted, back to the binary. The binary XOR operation tells you if you are in a winning or losing state. If you ended up with all zeros you are in a losing state. Take as few Hamsters as possible and wait for your opponent to make a mistake. However, if there are any 1s in the result, you are in a winning state. Better still you can make sure that you put your opponent into a losing state with your move by taking hamsters away in such a way that you turn the odd/even result into all 0s.

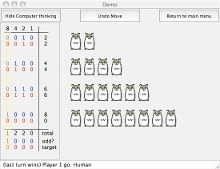
How do you do that? You need somehow to manipulate the bits in the columns that have 1s in (the columns with 0s in are fine so you don't want to change them at all). You can only change the number in one pile in your go, so you can only change one row (ie pile of hamsters). All you need to do is to flip the bits from 1 to 0 or from 0 to 1 in that row in each column where the result was a 1. That will turn it into a zero. The new binary number you end up with will tell you the number of Hamsters you need in that pile to make a winning position. For some piles these numbers will be bigger than the original number. You can't add hamsters to a pile only take away so that pile isn't any good. Try a different one. When you find a pile where flipping the bits lowers the number of Hamsters, that is the move to make.

Rather than trial and error you can actually work out which pile to use. We will leave you to work out that by watching our Hamster Master think.

So you should never lose at Nim again...as long as you make sure the numbers in the piles at the start leave you in a winning position of course.