Bean Counting

As the rest of the class frantically scribbled, ten year old Carl Gauss came to the front and presented his slate to the teacher. The teacher was furious: he had only just set the problem and had expected to have a whole lesson where he could just snooze. The problem involved adding up all the numbers from 1 to 100: that normally took the kids 30 or 40 minutes, not seconds - back then in 1787 there weren't even calculators just slates to write on, and even with a calculator it would take a while to work out the answer. Surely Gauss could not have worked it out so quickly...but his answer was right: 5050...and remarkably he hadn't needed any working. He had just written down the answer.

Algorithms: the rules of the game

How had Gauss done it? By lateral thinking. He had attacked the problem in a different way, to everyone else, seen a pattern and come up with a different route to the answer. Gauss is now hailed as a great Mathematician but in that lesson he was also dabbling in computer science long before computers were invented. At the core of computer science is the idea of algorithms - rules you can follow to complete some task...whether to recognize a pick-pocket in a CCTV picture, fly a plane or calculate an answer to a teacher's question. There can be many algorithms for the same task some faster than others. What Gauss had done was come up with a mathematical equation that allowed him to invent a faster algorithm than anyone else had previously thought of. It doesn't really matter whether the algorithm is to be followed by a person or a computer, so even though computers weren't invented, he was doing computer science.

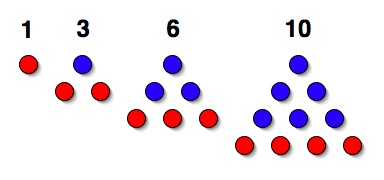
The problem the teacher had set was about triangular numbers...if you are arranging beans, coins or even floor tiles in a triangular pattern, how many do you need for a given sized triangle? The sequence goes 1, 3, 6, 10, 15, ... A triangle of side 1 is made of 1 bean, a triangle of side 2 needs 3 beans to make it, a triangle of side 4 needs 10 beans... This is just one of those "What comes next in the sequence?" problems. It's quite easy to work out the next number each time - you just add the previous answer to your current position in the sequence - so to get the sixth triangular number, you just add 6 to the previous answer (15) giving 21. To get the 7th in the sequence add 7 to 21, and so on. That is easy to do, if slow, and Gauss's teacher had asked what is the 100th number in the sequence...which is where adding all the numbers from 1 to 100 together comes in.

The trick

What Gauss had realized was that if you really were thinking about triangles with side 100, you could put two identical triangles together to make a rectangle and then ask how many beans were needed to make the rectangle. It has sides 100 by 101. To get the area of a rectangle you just multiply the sides. We are interested in just one of the two identical triangles making up the rectangle, so its area (number of beans) is half that of the rectangle - so we need to multiply 50 by 101 to get the answer. All Gauss had done was multiply 101 by 5 to get 505 and then stick a zero on the end...giving the answer in seconds.

The trick works for any triangular number. To get the 6th, think of two triangles of size 6 making a rectangle of sides 6x7. You want half that area, so multiply 3x7 to get 21. The trick can be expressed as a simple rule (the algorithm): For the nth triangular number just multiply n by (n+1) then divide by 2.

Whilst research computer scientist's may spend their time devising completely new and clever algorithms, thanks to geniuses of the past like Gauss there is a whole collection of tricks we already know about that computer scientist's can use. The trick to being a good computer scientist is not so much being able to think of revolutionary new ways of doing things (that would make you an exceptional computer scientist and probably famous), but being able to spot when an existing trick can be applied in the current situation - for the program you are trying to write now.

Once you know Gauss's trick - the fast algorithm - you can solve the problem as fast as he did working out any triangular number quickly...tiled floors R us! Shame there aren't more triangular floors needing tiling. It turns out though that triangular numbers have other uses for computer scientist's too - for example they are at the heart of one of the most common things computers are used to do - sorting data into order...but that is another story.