A magazine where the digital world meets the real world.
On the web
- Home
- Browse by date
- Browse by topic
- Enter the maze
- Follow our blog
- Follow us on Twitter
- Resources for teachers
- Subscribe
In print
What is cs4fn?
- About us
- Contact us
- Partners
- Privacy and cookies
- Copyright and contributions
- Links to other fun sites
- Complete our questionnaire, give us feedback
Search:
The French Peasant's Lock and Gray Code
The French Peasant's lock puzzle has appeared in lots of different forms: "The chinese rings" puzzle being the most famous. There is even a version with elephants to get in a line and march off.
The solution to the lock is actually something know to Computer Scientists as Gray Code: a code used in modern digital TV. Whatever, their physical form all the variations of the lock puzzle have the same solution and are logically (and so their solutions algorithmically) identical. Solve one and you've solved them all (Computer Scientist's love pulling that trick with problems!)
Each piece on the bolt can be of one of two kinds (it can be in one of two "states"): a disc or a sideways T. For simplicity let's refer to the discs as 0 and the T shapes as 1. Now every state of the bolt as a whole can be thought of as a series of 1s and 0s. The starting state has a single T at one end but otherwise is all zeros: the state 1 000 000. The end state when the bolt is free has all discs so is 0 000 000. The problem is to move from 1 000 000 to 0 000 000 by following the restrictions of the lock. They mean that only two pieces can be swapped at any time (either the end one or the piece immediately after the first T), but also that only a single 1 or 0 can be changed in any move. For example, the first move might be to flip the end piece from a disc to a T. We get new position 1 000 001. Only a single position (or bit as a computer scientist would call it) has changed.
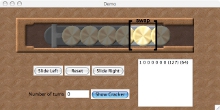
Agreeing what it all means
Computers represent all information like this as sequences as 1s and 0s. Not just states of a puzzle, but the characters making up a word processor document, the individual points or pixels in an image, the sounds in a downloaded track. Everything. That of course includes numbers too. Each kind of document holding information uses a code over what the 1s and 0s represent. The code in our puzzle is that 0 means a disc in that position and 1 means a T piece. For one computer to be able to share information with another they have to agree on the code - how to interpret the 1s and 0s. There are a whole series of standard codes. For example, with simple numbers computers mostly use a special sequence that counts 0=0000, 1=0001, 2=0010, 3=0011, 4=0100, and so on. This isn't an arbitrary code. It uses the same mechanism as we use for decimal numbers. If I write the number 340, what I mean is 3x100 + 4x10 + 0x1. Each position is a different power of 10. The system computers use is the same but you multiply by 2 not 10. So a number like 1001 in binary stands for the number 1x8 + 0x4 + 0x2 + 1x1 = 9. Using this coding our start position in the lock puzzle (1 000 000) is also the number 64. That shows too that a particular bit pattern can mean different things in different situations - it all depends on the code you use to unscramble it.
Counting made easy
The code above that computers normally use for numbers is great for most purposes - it is easy to work out what number a pattern of 1s and 0s stands for and to do arithmetic for example. It's not so good for other things though. Take counting: you sometimes have to change the bit pattern in lots of ways just to add one to the number it represents - for example to go from 7 to 8 means changing from 0111 to 1000. All four bits had to be changed. In some situations this can be a pain. If all you are using the numbers for is to count through a sequence it may be easier if you use a different code - one where moving on in the sequence only involves changing one bit. A code like this one: 0=0000, 1=0001, 2=0011, 3=0010, 4=0110 and so on. Codes like this that change one bit at a time are called Gray codes after Frank Gray, a physicist at Bell Labs, who first invented them.
Gray codes crop up in lots of different places, including in digital TV. There a code is needed for the pictures that are transmitted as well as for control information. Trouble is the information can be corrupted as it is transmitted, flipping bits occasionally making the message unreadable. It turns out though that with some extra, special tricks a Gray code has properties that make it possible to detect and correct cases when bits have been flipped - down to this property of things only changing by one bit only. So Gray codes are used in the way your digital TV signal is transmitted.
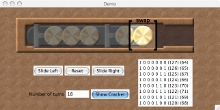
Gray coded puzzles
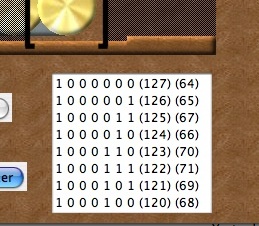
What has all that to do with our puzzle? Well the solution to our lock counts through a sequence in a way that, using our code, only changes one bit at a time: It is a Gray code. Use the normal binary numbering to convert the puzzle states to numbers though and the numbers jump about apparently randomly (the end sequence of numbers in the cracker): 64,65,67,66,70,71,69,68...It's of no use to help solve the puzzle. Convert the states to numbers using the Gray code as our cracker does too and suddenly there is a pattern: 127,126,125,124,123,,122,121,120, ... Make a wrong move and you can tell as the Gray code count goes up instead of down. I bet you can see how many moves the lock takes to open too! Want a harder lock to crack? Just add an extra disc or two. Very quickly the number of moves in the solution gets unimaginably big.
Who would have thought that a puzzle used by French peasants to protect their valuables would also be useful in protecting our TV pictures from corruption? Maybe Davy Jones should have used the same trick. After all, unlike mere mortals he had all the time in the world if he ever wanted to retrieve his heart from his chest. With a long enough Baguenaudier, even knowing the solution, Captain Jack Sparrow would have died long before opening it.


