Pixels and Puzzles

You must have heard it said that everything in a computer is just numbers: even pictures. When your digital camera takes a picture it converts the scene ("encodes" it) to a long list of numbers. When it displays it on the screen it is converting the numbers back into a picture ("decoding" them). But how is it done?

A simple way is to put a fine grid over the picture, and store a number corresponding to the colour of each square. With black and white pictures, 0 could be used for white and 1 for black. To get the picture back from the 1s and 0s (decode it), you just go through the grid, filling in the squares corresponding to 1s and leaving the 0's.

There are lots of different ways a picture could be stored as numbers though. The above is just the most obvious. Which way is best depends on what you are trying to do with them. There is no right way. That is why there are lots of different picture formats like "jpeg" and "gif". Each uses a different method, or "algorithm", for converting pictures to numbers and back again.

You might want to be able to draw the picture really quickly - in which case the method above is very good. Or, you might want to store as many pictures on your memory card as possible - which would mean you want the list of numbers to be as short as possible to get the same quality picture back. That would also mean the photo could be transmitted over the Internet much more quickly: as a web page, for example. Our encoding method above takes 100 numbers to store a 10x10 picture. Can you work out a way to store pictures with the same number of squares using fewer numbers?

The following puzzle uses an encoding of a picture where the aim is just for you to have fun while testing your logical skills. It only uses 57 numbers to store a 15x15 picture. Getting the picture back isn't easy though (but that's what makes it fun)!

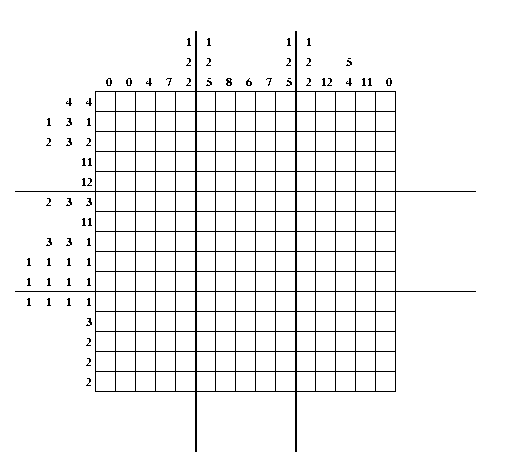
Here is a version to print (in pdf).

The numbers on each row (or column) tell you the number of black cells in the row (column), in each group of black cells. So if the numbers next to a row are 2,4,5 it means that row has a block of 2 black cells, a block of 4 black cells and a block of 5, in that order. Each block is separated by one or more white cells. Columns are encoded in the same way.

This puzzle's algorithm wouldn't work as a way of encoding pictures in your camera because there are some pictures that share the same sequences of numbers. That means you wouldn't be able to decode them to a unique picture. A set of numbers could have started out as ony one of several pictures. Can you work out the simplest picture that can't be uniquely decoded? The challenge for computer scientists is to devise ways that always give a unique picture back that looks no different to the original, that uses as few numbers as possible but that also gets the picture back as quickly as possible. An impossible dream? One for you to solve.

Don't look at the answer until you have had a go at solving it.